很偶然地, bartoli的结果被玻尔兹曼知道了.玻尔兹曼是奥地利物理学家,是热力学和统计物理学的奠基人之一.1866年在维也纳大学时,在stefan的指导下写了一篇论文a thesis on the kinetic theory of gases获得博士论文,之后成为stefan的助手,之后再由stefan的推荐,成为某校教授.
玻尔兹曼在分析了bartoli 的结果后,得到辐射压
$$p = \frac{1}{3}u$$u表示辐射能量密度.再利用基本热力学关系
$$dU = TdS - pdV$$以及辐射能量密度
$$u = \frac{U}{V}$$得到了stefan根据实验所得的公式(具体参考wikipedia),Bartoli和boltzmann将电磁学和热力学结合起来处理热辐射的想法被Wien使用.Wien的推导过程是用了多普勒效应,我们先来认识多普勒效应.
Stars are suns,距离地球遥远的星星是一些类似太阳的发光发热的恒星,它们在宇宙中高速运动.但为什么有些星星是橘黄色的orange,其它一些又是红色或蓝色的?这种颜色的不同在特定联星中尤其突出.联星是指两颗星,它们绕由其组成的系统的质心运动.1842年,澳大利亚天文学和数学家,Prague大学教授多普勒doppler觉得他找到了一种解释.
根据多普勒的解释,光是一种波动现象,我们看到的光的颜色是由光的频率决定的.这个频率依赖于光源和观察者之间的相对运动速度.如果光源和观察者相互靠近,每秒钟达到观察者的光波就更多,观察到的频率就会更高,所以光的颜色将会变得更绿.如果观察者和光源之间的距离不停地增加,观察到的频率就会减小,观察者就会看到更红的颜色.
1842年5月25日,doppler在Prague大学进行了一场演讲,在演讲中解释了他的如上理论,一年后,这个理论被发表.多普勒还提到,同样的效应在声波中也应该可以被观察到.多普勒效应在声波上于1845年被ballot验证,但是不能用来解释恒星颜色的不同,因为颜色的不同是由于不同表面温度造成的.联星的颜色不同主要是由于相互之间的对比、差异造成的.然而多普勒效应在现代天文学中依然十分重要.天体的旋转和运动可以通过它们发出的光的微小变化计算出来.
德国物理学家维恩(Wilhelm Carl Werner Otto Fritz Franz Wien,1864年-1928年)1864年1月13日出生在东普鲁士(现俄罗斯)的菲施豪森(Fischhausen),他的父亲卡尔•维恩(Carl Wien)是地主.1879年在拉斯滕堡(Rastenburg)、1880年至1882年在海德堡读中学.中学毕业后,1882年在哥廷根大学学习数学,同年转去柏林大学(德国当时学生有到不同学校学习的惯例).1883年至1885年在亥姆霍兹的实验室工作,1886年获得博士学位,论文题目是光对金属的衍射(他的导师就是研究这方面的),以及不同材料对折射光颜色的影响.此后,由于维恩的父亲生病,维恩不得不回去帮助管理他父亲的土地(维恩和他父亲一样性格内向).期间他有一个学期跟随亥姆霍兹,1887年完成了金属对光和热辐射的导磁性实验.
在国家物理工程研究所,维恩与路德维希•霍尔伯恩(Ludwig Holborn)一起研究用勒沙特列(Le Chatelier)温度计测量高温的方法,同时对热动力学进行理论研究,尤其是热辐射的定律.1893年,维恩提出波长随温度改变的定律,后来被称为维恩位移定律.
黑体的辐射是由一个波长范围的辐射组成的,基尔霍夫已经给出黑体辐射是频率和温度两个变量的函数,所以当温度一定时,我们就可以测量辐射能量与频率的关系,借助光谱分析,我们可以测量频率与辐射的关系.将辐射集中在分光计的狭缝使其分散为光谱(this cannot be done with a prism of ordinary glass which absorbs strongly above some 2μm,但是可以用rock salt prism).可以通过放置热电偶在不同波长的位置来研究.在光谱的任意一点上,热电偶接头截取到波长范围为λ到△λ内的能量,这个能量除以△λ,商就是单位波长的能量.如果我们测量发射的能量与发射面积的比值,我们就可以得到单位波长范围的辐射出射度Mλ.
19世纪末期时像这样的测量已经做完了,产生了类似下图的曲线图:
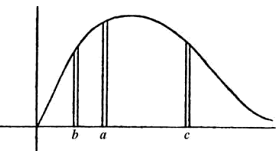
横坐标表示波长,纵坐标表示能量密度(reprinted from Wien copyright(1894))复制于Wien1894年发表的论文中,说明Wien曾经做过这个实验.
Wien的想法是使用一个有一个小洞的像烤炉一样的物体近似模拟黑体,通过小洞进入黑体的辐射经过内壁的散射和反射,从而几乎所有进入火炉的辐射都被吸收了,那些找到路径再次射出烤炉的辐射会非常少,于是从小洞出来的辐射就非常接近黑体达到平衡状态时与其温度对应的电磁辐射.(这种模型基尔霍夫曾经给出过.)
Wien发现,温度不变时,单位波长范围dλ的辐射能量dW在某一特定波长λm处有一个最大值,随着温度的增加,这个最大值所处的波长λm向短波方向移动,他发现λmT是一个常量,λmT=0.2898 centimetre-degree Kelvin.
温度增加时辐射能量的最大值向更高频率移动的Wien位移定律以量的形式表达了我们平常观察到的情况.我们的皮肤感觉温暖的物体会产生红外辐射;温度接近T=950 K会观察到昏暗的红光;温度增加时,光的颜色会增强,变成橘黄色和黄色.钨丝灯的温度是T=2500 K会发出白光,但是根据Wien的定律,此时光谱的最大值依然是红外的,当温度达到T=6000 K时,光谱的最大值移向可见的黄色,就像太阳表面的颜色一样.
Wien的定律只是一个通过实验得到的经验公式而不是理论推导得到的.1894年,Wien通过一个思想实验thought experiment进行了理论推导.
Wien研究了由两个过程导致的辐射能量密度的增加:温度的增加和绝热情况下含有辐射的密闭体积的减小.如果这两个过程最终都达到相同的温度,那么both process should lead to the same energy distribution among the wavelengths.在考虑了多普勒效应后,他达到了这个目标.
想象一个装有黑体辐射的圆柱体被一个能够完全反射辐射的可移动的活塞封闭,移动活塞,我们可以缓慢地减小圆柱体空腔的体积,从而这种压缩过程是绝热的,也就是说,平衡态始终被保持着,被活塞反射的辐射的频率将根据多普勒效应而变化,因此由于活塞的运动做功,这个封闭空间内的温度将上升,定量的变化过程使得Wien得到了Wien位移定律. 具体过程参阅:Theoretical Concepts in Physics: An Alternative View of Theoretical Reasoning in Physics,page 297 to page 302.
