所谓概率，其实就是可能性.气体里的大量运动分子，总是有的向东有的向西，各个方向都有.对于某个分子而言，它向哪个方向运动都有可能，也就是都有一定的概率.但由于条件的限制，分子在不同方向上运动的概率是不同的.如果我们确定了这些概率，我们就能运用统计规律，得出相应的结果.例如，对于包围你的室内空气而言，就可以计算每个空气分子所有可能的分布方式及其所有可能的运动方式.这就是玻尔兹曼的思想——用统计理论来解释热力学问题，这在当时的物理学界引起了很大的争议.但事实证明，玻尔兹曼是对的.

要在热力学中计算分子处于某个微观状态的概率，首先要计算体系中粒子可能具有的所有不同微观状态的总数，它是一个非常大的数.在1877年的论文中，玻尔兹曼发现了微观状态数与宏观系统的克劳修斯熵之间的关系，并用下面这个关系式把它们联系了起来：

$$S \propto \ln W$$

微观状态：系统中每一个微粒的各种状态量，比如位置，动量等.

宏观状态：系统的宏观描述，比如P，V，或者速率在某一范围内的粒子数量等.

一般来说，宏观状态包含了大量的微观状态.例如，一个容器内含有2个气体分子，我们想确认这两个气体分子在容器的左边还是右边，

宏观状态：3种：一左一右，左左，右右

微观状态：4种：LL， RR， LR， RL

3个分子时，

宏观状态：4种

微观状态：8种：LLL， (LLR， LRL， RLL)， (LRR， RLR， RRL)， RRR

4个分子时，

宏观状态：5种

微观状态：16种：(all L) (3L， 1R) (2L， 2R) (1L， 3R) (all R)

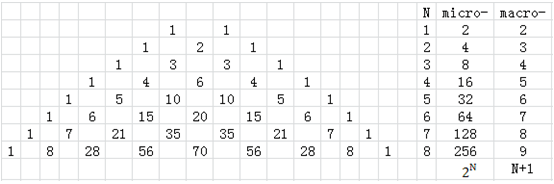
左上表可以用组合数来给出，即从N个元素中任意拿出2个，一共有多少种组合，

$${W_{N,n}} = \frac{{N!}}{{n!\left( {N - n} \right)!}},{W_{6,2}} = \frac{{6!}}{{2!4!}} = 15$$

问题1：从字母a，b，c中任选两个组合，有多少种不同的选法?

ab ，ac，bc 无顺序

问题2：从字母a，b，c中任选两个排成一列，有多少种不同的选法?

$A_3^2 = 6$有顺序

组合的定义：

从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数.用符号

$$C_n^m$$

表示.

排列的定义：

从n个不同元素中，任取m(m≤n)个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数.用符号

$$A_n^m$$

表示.

排列与组合的异同：

排列与元素的顺序有关，而组合则与元素的顺序无关.

写出从a，b，c，d四个元素中任取三个元素的所有组合.

abc

abd

acd

bcd

写出从 a，b，c，d四个元素中任取三个元素的所有排列.

求$A_4^3$可分两步考虑：

第一步，$C_4^3 = 4$

第二步，$A_3^3 = 6$

根据分步计算的原理：

$$A_4^3 = C_4^3 \cdot A_3^3$$