巴尔末是数学家，但是在数学领域没有让人记住的成就.在巴塞尔大学兼任讲师期间，年近60岁的巴尔末受到该校一位研究光谱的物理学教授哈根拜希（E.Hagenbach）的鼓励，开始试图寻找氢原子光谱的规律.当时氢光谱见光区波段的4条谱线已经过埃姆斯特朗等人的精确测定.巴尔末找到了一个数学公式来表达这四条谱线的波长，以及Huggins通过观察恒星得到的紫外区的10条氢光谱线的一共14条氢谱线的波长的经验公式，他还推测可能有额外的谱线在氢的光谱中，其他谱线及其波长被其他科学家发现了.

埃格斯特朗Ångström测量了氢光谱线的波长，而巴尔末的公式显示这些波长不是随机的.用一个数学公式表达氢原子光谱谱线波长的规律改变了科学家们对光谱线的思考方式.在巴尔末之前，科学家们将光谱线与musical harmonies相类比，认为在谱线之间有简单的harmonic ratios.巴尔末之后继续在女子中学教数学，完全没有意识到他在氢的光谱上的工作使他在科学上immortality.20世纪初期，德国物理学家普朗克为解释黑体辐射现象，提出了量子理论，揭开了量子物理学的序幕.19世纪末，瑞士数学教师巴耳末将氢原子的谱线表示成巴耳末公式

$$\eqalign{ & \lambda = B\left( {\frac{{{n^2}}}{{{n^2} - {m^2}}}} \right) = B\left( {\frac{{{n^2}}}{{{n^2} - {2^2}}}} \right) \cr & B = {\text{3}}.{\text{645}}0{\text{682}} \times {\text{1}}{0^{ - {\text{7}}}}{\text{m}}{\text{or}}{\text{364}}.{\text{5}}0{\text{682}}{\text{nm}} \cr} $$

瑞典物理学家里德伯总结出更为普遍的光谱线公式里德伯公式：

$$\eqalign{ & \frac{1}{\lambda } = R\left( {\frac{{{n^2}}}{{{n^2} - n{'^2}}}} \right),n = 1,2,3,...; \cr & n' = n + 1,n + 2,n + 3,... \cr & R = 4/B \cr} $$

其中λ为氢原子光谱波长，R为里德伯常数.

然而巴耳末公式和里德伯公式都是经验公式，人们并不了解它们的物理含义.

1911年，英国物理学家卢瑟福根据1910年进行的α粒子散射实验，提出了原子结构的行星模型.在这个模型里，电子像太阳系的行星围绕太阳转一样围绕着原子核旋转.但是根据经典电磁理论，这样的电子会发射出电磁辐射而损失能量，以至瞬间坍缩到原子核里.这与实际情况不符，卢瑟福无法解释这个矛盾.

1912年，正在英国曼彻斯特大学工作的玻尔将一份被后人称作《卢瑟福备忘录》的论文提纲提交给他的导师卢瑟福.在这份提纲中，玻尔在行星模型的基础上引入了普朗克的量子概念，认为原子中的电子处在一系列分立的稳态上.回到丹麦后玻尔急于将这些思想整理成论文，可是进展不大.

1913年2月4日前后的某一天，玻尔的同事汉森拜访他，提到了1885年瑞士数学教师巴耳末的工作以及巴耳末公式，玻尔顿时受到启发.后来他回忆到“就在我看到巴耳末公式的那一瞬间，突然一切都清楚了，”“就像是七巧板游戏中的最后一块.”这件事被称为玻尔的“二月转变”.

1913年7月、9月、11月，经由卢瑟福推荐，《哲学杂志》接连刊载了玻尔的三篇论文，标志着玻尔模型正式提出.这三篇论文成为物理学史上的经典，被称为玻尔模型的“三部曲”.

玻尔理论本身仍是以经典理论为基础，且其理论又与经典理论相抵触.它只能解释氢原子以及类氢原子（如锂+离子，等）的光谱，在解决其他原子的光谱时就遇到了困难，如把理论用于其它原子时，理论结果与实验不符，且不能求出谱线的强度及相邻谱线之间的宽度.这些缺陷主要是由于把微观粒子(电子，原子等)看作是经典力学中的质点，从而把经典力学规律强加于微观粒子上(如轨道概念)而导致的.

“玻尔理论”的提出，打破了经典物理学一统天下的局面，开创了揭示微观世界基本特征的前景，为量子理论体系奠定了基础，这是一种了不起的创举，不愧为爱因斯坦的评价－－玻尔的电子壳层模型是思想领域中最高的音乐神韵.

玻尔模型的难点在于角动量量子化条件的得出，即

$$L = \frac{{nh}}{{2\pi }} = n\hbar $$

如何得到的？

这个问题的解释需要如下知识点：

1. 电磁波携带角动量；

2. 电磁辐射的能量是量子化的；

3. 光电效应和光子理论.

这里主要讨论第一个知识点.

所有其它我们已经学过的波（声波，纵向弹簧波，横向绳波）都不携带动量，与这些熟悉的波类比，很难明显地看出电磁波带有动量，电磁波很可能只带有能量而不带有动量.

我们根据狭义相对论来快速地讨论一下为什么电磁波带有动量.根据狭义相对论，$E = m{c^2} = pc$，可知光子的动量是，$p = E/c$.我们已知电磁波带有能量E，因此这个关系式告诉我们电磁波也带有动量.这样的讨论是完全正确的，但不是很令人满意.首先这个讨论包含狭义相对论的内容.其次还包含了将电磁波（光）看作是由称为光子的微观粒子组成的事实.

为什么光的粒子性是导出电磁波带有动量的必要条件呢？我们希望能够只用波的概念和目前已经学过的波的特性来导出$p = E/c$的结果.

现在考虑一个带有电量q的粒子在某种物质中运动，使其受到一束电磁波的影响，这个微粒将受到组成电磁波的电场E和磁场B的作用力，也还会受到周围物质的力的阻尼作用，且这个粒子还会因为加速度而产生辐射，因而损失能量，但是辐射和阻尼作用在我们的讨论中不重要.

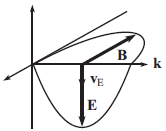
假设这个电磁波沿着z轴的正向传播，E沿着x轴正向，因为$E \times B \propto k$，于是B指向y轴正向，带电粒子的运动通常来说是很复杂的，但是就现在讨论的目的而言，只需考虑粒子的x轴方向的速度分量就足够了，也就是说，这个分量平行于电场E.由于电场的振荡，带电粒子也会沿着E的方向向前向后振荡（主要沿着这个方向振荡），不过我们并不知道振荡的相位，通常来说，带电粒子的速度将部分与E同相位，部分与E有±90°的差异，后面这部分与我们的讨论无关，所以只需要集中考虑与E同相位的速度即可，我们称之为${v_E}$,如下图所示

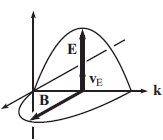
半周期后