时间膨胀可以根据狭义相对论的第二个假设，即：对所有观测者来说，光在真空中的速度都是相同的，与光源的运动无关.

光速不变意味着，与直觉不同，光速与有质量的物体的速度没有可加性，即两者的速度不能相加.通过远离光源或靠近光源使得光速变慢或变快是不可能的.

考虑这样的情景，以速度v向右做匀速直线运动的，高度为L的车厢顶部有一块平面镜，一束光从车厢底部垂直射向顶部的平面镜.

1. 在车厢内的静坐的观察者看来，光经过的路径为2L，所用的时间为

$$t = \frac{{2L}}{c}$$

2. 在车厢外静止的观察者看来，光经过的路径为

$$2D = 2\sqrt {{L^2} + \frac{1}{2}t'} $$

所用的时间为

$$\eqalign{ & t' = \frac{{2D}}{c} = \frac{{2\sqrt {{L^2} + {{\left( {\frac{1}{2}t'v} \right)}^2}} }}{c}, \cr & t{'^2} = \frac{{4\left( {{L^2} + \frac{1}{4}t{'^2}{v^2}} \right)}}{{{c^2}}}, \cr & 4\left( {{L^2} + \frac{1}{4}t{'^2}{v^2}} \right) = t{'^2}{c^2} \cr & 4{L^2} + t{'^2}{v^2} = t{'^2}{c^2} \cr & t' = \sqrt {\frac{{4{L^2}}}{{{c^2} - {v^2}}}} \cr} $$ $$\eqalign{ & t' = \sqrt {\frac{{4{L^2}}}{{{c^2} - {v^2}}}} = \sqrt {\frac{{{t^2}{c^2}}}{{{c^2} - {v^2}}}} \cr & = \frac{{tc}}{{\sqrt {{c^2} - {v^2}} }} = \frac{t}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} \cr} $$

即

$$t' = \frac{t}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}$$

由于$0 < \frac{{{v^2}}}{{{c^2}}} < 1$，所以$t' > t$，假如$\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} = \frac{1}{2}$，则$t' = 2t$，对于运动的人来讲，，他们观察到自己的时钟走了10年时，对地面静止的人来说，观察到的时钟已经走了20年，于是会说，你们运动的时钟变慢了，本来应该走了20年，可是只走了10年.一个在地球人看来星际旅行了20年的人回到地球，地球人会发现他的时钟只走了10年，人也只老了10岁，而他看到的地球人已经老了20岁了.注意，这是以地球为静坐参考系推导出来的.

考虑这样的情景，以速度v向右做匀速直线运动的，长度为L的车厢前后有2块平面镜，一束光从车厢后部向前直射向前部的平面镜.

车厢内静止的人测得光束经过的路程为$D = 2{L_0} = c{t_0}$，车厢长度为${L_0} = \frac{{c{t_0}}}{2}$.

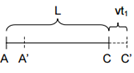
对于站在车厢旁边地面上的人看来，设光束向前射到车厢前部所用时间为${t_1}$，从前部的镜子反射回到后部所用时间为${t_2}$，光束来回所用时间$t = {t_1} + {t_2}$，

$$\eqalign{ & L + v{t_1} = c{t_1} \Rightarrow {t_1} = \frac{L}{{c - v}} \cr & L - v{t_2} = c{t_2} \Rightarrow {t_2} = \frac{L}{{c + v}} \cr & t = {t_1} + {t_2} = \frac{L}{{c - v}} + \frac{L}{{c + v}} = \frac{{Lc + Lv + Lc - Lv}}{{{c^2} - {v^2}}} = \frac{{2cL}}{{{c^2} - {v^2}}} = \frac{{2L}}{c}\frac{1}{{1 - \frac{{{v^2}}}{{{c^2}}}}} \cr & L = \frac{{ct}}{2}\left( {1 - \frac{{{v^2}}}{{{c^2}}}} \right) \cr} $$

根据时间膨胀的结论

$$t = \frac{{{t_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}$$

，得

$$L = \frac{c}{2}\left( {1 - \frac{{{v^2}}}{{{c^2}}}} \right)\frac{{{t_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \frac{{c{t_0}}}{2}\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} $$

结合

$${L_0} = \frac{{c{t_0}}}{2}$$

得